Perbezaan Antara Derivatif dan Pembezaan

Derivatif vs Berbeza

Dalam kalkulus diferensial, derivatif dan pembezaan fungsi adalah berkait rapat tetapi mempunyai makna yang sangat berbeza, dan digunakan untuk mewakili dua objek penting matematik yang berkaitan dengan fungsi yang berbeza.

Apa derivatif?

Derivatif fungsi mengukur kadar di mana nilai fungsi berubah apabila perubahan inputnya. Dalam fungsi pelbagai variabel, perubahan dalam nilai fungsi bergantung kepada arah perubahan nilai-nilai pembolehubah bebas. Oleh itu, dalam keadaan sedemikian, arah tertentu dipilih dan fungsi dibezakan dalam arah yang tertentu. Derivatif itu dipanggil derivatif arah. Derivatif separa adalah jenis derivatif arah khas.

Derivatif fungsi bernilai vektor f boleh ditakrifkan sebagai had

di mana ia wujud dengan tepat. Seperti yang dinyatakan sebelum ini, ini memberi kita kadar peningkatan fungsi f di sepanjang arah vektor u. Dalam kes fungsi tunggal yang bernilai, ini akan mengurangkan takrifan terkenal dari derivatif,

Sebagai contoh,

adalah di mana-mana berbeza, dan terbitannya sama dengan had,

, yang bersamaan dengan

. Derivatif fungsi seperti

wujud di mana-mana. Mereka masing-masing bersamaan dengan fungsi

.

Ini dikenali sebagai derivatif pertama. Biasanya derivatif fungsi pertama f dilambangkan oleh f ⁽¹⁾ . Sekarang menggunakan notasi ini, adalah mungkin untuk menentukan derivatif pesanan yang lebih tinggi.

adalah derivatif arah urutan kedua, dan menandakan derivatif n ^th dengan f ⁽ⁿ⁾ n,, mentakrifkan

n th ^derivatif. Apakah perbezaannya?

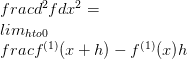
Pembezaan fungsi mewakili perubahan dalam fungsi berkenaan dengan perubahan dalam pembolehubah bebas atau pembolehubah. Dalam notasi biasa, bagi fungsi yang diberikan

f bagi pembolehubah tunggal x, jumlah perbezaan pesanan 1 df diberikan oleh,. Ini bermakna bahawa untuk perubahan kecil

x (iaitu d x), akan terdapat f (1) ⁽ x <) d x perubahan dalam f. Menggunakan had satu boleh berakhir dengan definisi ini seperti berikut. Anggap Δ x

adalah perubahan x pada titik sembarangan x dan Δ f f. Ia boleh ditunjukkan bahawa Δ f = f (1) (x ^{) Δ} x + ε, kesilapan itu. Sekarang, had Δ x → 0 Δ f / ^{Δ x} = _{f (1) (} x) (menggunakan definisi derivatif yang dinyatakan sebelumnya) dan oleh itu, Δ ^{x →} 0 ε / Δ x = 0.Oleh itu, adalah mungkin untuk membuat kesimpulan bahawa, ^{x →} 0 _{ε = 0. Sekarang, menandakan Δ} x → 0 Δ f sebagai d f dan Δ x → 0 Δ x sebagai d x definisi pembezaan diperolehi dengan ketat. Sebagai contoh, perbezaan fungsi adalah. Dalam kes fungsi dua atau lebih pemboleh ubah, jumlah pembezaan fungsi ditakrifkan sebagai jumlah perbezaan dalam arah setiap pembolehubah bebas. Secara matematik, ia boleh dinyatakan sebagai.

Apakah perbezaan antara derivatif dan perbezaan?

• Derivatif merujuk kepada suatu kadar perubahan fungsi manakala pembezaan merujuk kepada perubahan fungsi sebenar, apabila pembolehubah bebas berubah.

• Derivatif diberikan oleh, tetapi pembezaan diberikan oleh

.

Disyorkan Perbezaan Antara Dunia dan Bumi Perbezaan Antara Bank Dunia dan IMF Perbezaan Antara Worldview dan Ideology | Worldview vs Ideology