Perbezaan Antara Integrit dan Indefinite Integrals Perbezaan Antara

Kalkulus adalah cabang matematik yang penting, dan pembezaan memainkan peranan penting dalam kalkulus. Proses songsang pembezaan dikenali sebagai integrasi, dan sebaliknya dikenali sebagai integral, atau hanya meletakkan, kebalikan dari pembezaan memberikan integral. Berdasarkan hasil yang mereka hasilkan, integral dibahagikan kepada dua kelas iaitu., integral pasti dan tak terbatas.

Definite Integral

- f (x)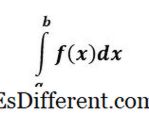

adalah NUMBER dan mewakili kawasan di bawah kurva f (x) dari x = a ke x = b . Integral pasti mempunyai had atas dan bawah pada integral, dan ia dipanggil pasti kerana, pada akhir masalah, kita mempunyai nombor - itu adalah jawapan yang pasti. - Integral yang tak tentu dari f (x) adalah FUNGSI dan menjawab soalan, "Apa fungsi apabila dibezakan memberikan

f (x)

? "

Dengan integral tidak terbatas tidak ada batasan atas dan bawah pada integral di sini, dan apa yang akan kita dapatkan adalah jawapan yang masih ada

x di dalamnya dan juga akan tetap (biasanya ditandakan dengan C) di dalamnya.

Integral tak terbatas biasanya memberikan penyelesaian umum kepada persamaan pembezaan. Integral tidak terbatas adalah lebih daripada satu bentuk integrasi umum, dan ia boleh ditafsirkan sebagai anti-derivatif fungsi yang dipertimbangkan. Anggap pembezaan fungsi

F

mengarah ke fungsi lain

f, dan integrasi f memberikan integral. Secara simbolik, ini ditulis sebagai F (x) = ∫ƒ (x) dx atau F = ∫ƒ dx di mana kedua

F

dan

ƒ < adalah fungsi

x , dan F adalah berbeza. Dalam bentuk di atas, ia dipanggil Reimann integral dan fungsi yang dihasilkan mengiringi pemalar sewenang-wenangnya. Integral tidak selalunya sering menghasilkan keluarga fungsi; Oleh itu, integral tidak terbatas. Proses integral dan integrasi adalah di tengah-tengah menyelesaikan persamaan kebezaan. Bagaimanapun, tidak seperti langkah-langkah pembezaan, langkah-langkah dalam integrasi tidak selalu mengikut rutin yang jelas dan standard. Kadang-kala, kita melihat bahawa penyelesaian itu tidak dapat dinyatakan dengan jelas dari segi fungsi asas. Dalam hal ini, penyelesaian analitik sering diberikan dalam bentuk integral tidak terbatas. Teorema asas Kalkulus Integral yang pasti dan tidak pasti dikaitkan dengan Teorem Asas Kalkulus seperti berikut: Untuk mengira integral pasti, cari

integral tidak terbatas > (juga dikenali sebagai anti-derivatif) fungsi dan menilai pada titik akhir

x = a

dan x = b . Perbezaan antara integral pasti dan tidak pasti akan terbukti apabila kita menilai integral untuk fungsi yang sama. Pertimbangkan integral berikut: OK. Mari kita lakukan kedua-dua mereka dan lihat perbezaannya. Untuk penyepaduan, kita perlu menambahkan satu kepada indeks yang membawa kita kepada ungkapan berikut: Pada masa ini C

hanyalah konstan kepada kita. Maklumat tambahan diperlukan dalam masalah untuk menentukan nilai yang tepat

C

Marilah kita menilai integral yang sama dalam bentuk yang pasti i. e., dengan had atas dan bawah termasuk.

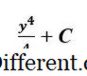
y = 2 dan y = 3 y = 2 dan

y = 3 >.

Langkah pertama dalam penilaian ini adalah sama dengan penilaian integral tidak terbatas. Satu-satunya perbezaan adalah bahawa kali ini kita tidak menambah C ^malar. Ungkapan dalam hal ini kelihatan seperti berikut: Ini berpaling membawa kepada: Pada dasarnya, kita menggantikan 3 dan kemudian 2 dalam ungkapan dan memperoleh perbezaan di antara mereka. Ini adalah nilai yang pasti berbanding penggunaan C

yang lebih awal. Mari kita meneroka faktor pemalar (berkaitan dengan integral tidak terbatas) dalam beberapa butiran lanjut. Jika

y

3

adalah 3y

2 , maka 2

dy = y

3 Walau bagaimanapun, ^3y 2 boleh menjadi perbezaan banyak ungkapan yang termasuk ^y 3

-5 , > y ³ +7 ^{, dan lain-lain … Ini menunjukkan bahawa pembalikan itu tidak unik kerana pemalar tidak diketahui semasa operasi.}

Jadi pada umumnya, 3y ² adalah perbezaan y ³ + C di mana C ^{Secara kebetulan, C dikenali sebagai penyepaduan} '' integrasi .

Kami menulis ini sebagai: ∫ ^3y 2 . dx = y ³ + C Teknik penyepaduan untuk integral yang tidak pasti, seperti lookup meja atau integrasi Risch, boleh menambah ketakselanjaran baru semasa proses penyepaduan. Ketidakseimbangan baru ini muncul kerana anti-derivatif boleh memerlukan pengenalan logaritma kompleks. Logaritma kompleks mempunyai keterlambatan melompat apabila hujah melintasi paksi sebenar negatif, dan algoritma integrasi kadangkala tidak dapat mencari representasi di mana lompatan ini dibatalkan.

Sekiranya integral pasti dinilai oleh pengkomputeran pertama yang tidak penting dan kemudian menggantikan sempadan integrasi ke dalam hasilnya, kita harus sedar bahawa integrasi tidak tentu mungkin menghasilkan ketakselanjaran. Sekiranya ia, selain itu, kita mesti menyiasat kekurangan dalam selang integrasi.